AMS talk 10/24/15

About two months ago I gave a talk at the AMS Fall Western Sectional Meeting.  While I could have safely rehashed my QPL talk, I decided to push forward instead.  That may or may not have been the best idea – the results were certainly less polished.  On the other hand, I was able to describe controllability and observability of a control system in terms of string diagrams.  This is something that was painfully missing from my QPL talk’s results in July.  Seeing the nontrivial constants in the string diagrams the quantum folk were using provided the key insight, and I wanted to capitalize on it as soon as possible.

The punchline of the AMS talk is that the duality between controllability and observability noticed by Kalman in the late 50s and early 60s can be expressed in terms of a PROP, which is a kind of symmetric monoidal category.  In particular, this PROP includes a subPROP of finite-dimensional vector spaces and linear relations, which is basically what Paweł Sobociński deals with here under the name of Interacting Hopf monoids.  Okay, so the actual punchline is that the duality Kalman noticed six and a half decades ago between controllability and observability? it’s simply time-reversed bizarro duality.

Bizarro is Sobociński’s term (seen in episode 7 of his blog), but I’m kind of partial to it.

Grading exams (a modest^H^H^H^Hck proposal)

Exams are some of the most time-consuming parts of being an instructor.  They have to be written, proctored, and finally graded.  Given a class of students, it seems reasonable to expect that writing a free-response exam would be a 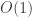time commitment, proctoring would also be a 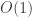time commitment, while grading would be a 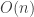time commitment.  Maybe grading speeds up as you get familiar with the particular set of mistakes your class makes, so I might believe something like  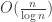instead of 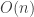.  In any case, asymptotically, grading takes a much greater share of time consumed than the other portions of the process combined.

With this in mind, I propose the following as a way of reducing the amount of necessary time spent in the grading process, while still giving a reasonable estimate of student understanding.  At least for a game theory class.

Game theory final exam (proposed)

(1) (100 points) Your score on this exam will be based entirely on this one question.  If is your answer and no one in this class answers with a greater number, 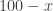will be your score.  Otherwise, will be your score.
_____

It is interesting to think about the possible strategies one may devise, which, for the student taking the exam, may depend on the class size and/or the student’s grade going into the final exam.  While it is fun to ponder, I will leave that as food for thought for the time being save that discussion for the comments.  Hopefully it will be clear that this isn’t entirely a serious proposal for an actual basis for grading a class, as forcing the entire class into a final exam that somewhat resembles the prisoner’s dilemma would be somewhat cruel.  There are some variations that may or may not be as evil:

Variation 1 (Unlimited collaboration)

The students are told in advance what the exam problem will be.  Thus, they are free to collaborate with as many of their classmates as they would like in order to come up with a strategy.  However, they cannot see what answers are actually submitted by their classmates.  This variation might be more evil.

Variation 2 (Limited collaboration)

The students are paired up and are allowed to discuss strategy only with their partner.  They may be able to see what their partner submits, but they have no information about what anyone else does.

Variation 3 (Multitrack)

The students are given the option to take one of two exams.  The first choice is the proposed exam above.  The wording could be modified slightly to restrict from the entire class to the subset of the class that chooses that choice.  The second choice is a standard final exam.  For the student who thinks, “I just need 50% on the exam to get the grade I want.”, it seems plausible for that student to take the first choice and write 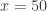for a guaranteed score and a personal 3 hour savings.

Other thoughts

I thought about this game while grading some calc exams.  It turned out there were quite a few people who incorrectly solved the problem I was grading, yet according to my rubric, their score was exactly the answer they wrote down.  Purely a coincidence, but it sparked the thought that led me to this game.  I showed this game to a few people yesterday, and the first two variations directly came from some of those discussions.  One person I showed immediately declared, “I don’t want to play this game!”.  Between the game and the variations, the multitrack variation seems the most reasonable to even consider actually giving.  Concerning the title of this post – computer printouts (in some contexts) used to display ^H when the user hit the backspace key.  Thus, it is meant to indicate the previous characters are being stricken out.